Introduction

In the previous blogpost we learned about the general concept of White-Box Cryptography, the reasons why it is gaining more presence in the world of mobile apps and its main advantages. However, like any other security measure, it is not perfect, and it exist scenarios where it can be defeated if the correct techniques are applied.

In this blogpost we will detail the two main attacks that are applied nowadays against White-Box Cryptography. We will look at their capabilities and limitations, and how to defend against them.

Main attacks against White-Box Cryptography

As explained in the previous post, since the late 1990s, it is known that some types of attacks traditionally used for hardware cryptographic implementations can be migrated to software by applying the same approach. The most effective attacks are:

• Differential Fault Analysis (DFA): DFA comes from a hardware background, and it is based in the injection of faults during the execution of a cryptographic algorithms to reveal their internal states.
• Differential Computational Analysis (DCA): DCA is the software derived version of the Differential Power Analysis (DPA) hardware attack and it is based in the mathematical analysis of the intermediate states of the algorithm to find correlations.

It is important to note that in order to implement these attacks some pre-requisites have to be met:

• The White-Box Cryptography implementation has to be identified in the binary and isolated to be run in an emulator. Running it in an emulator allows extraction of execution traces from memory and / or CPU registers.
• Control over the input / output of the White-Box Cryptography implementation to supply arbitrary inputs (e.g. plaintext) and retrieve the outputs (e.g. ciphertext).
• The cryptographic algorithm that is embedded in the White-Box Cryptography implementation has to be known for a proper mathematical analysis of the traces.

About this last point, we are going to use the Data Encryption Standard (DES) algorithm as example to understand how these attacks work, but it can be applied to other symmetric encryption algorithms such as AES.

Data Encryption Standard (DES)

The DES algorithm has 16 rounds where the same operations are performed using in each round a different subkey of 48 bits (plus 8 bits of redundancy) that is generated from the original secret key by applying a key scheduling algorithm. The following figure shows the flow of the DES algorithm.

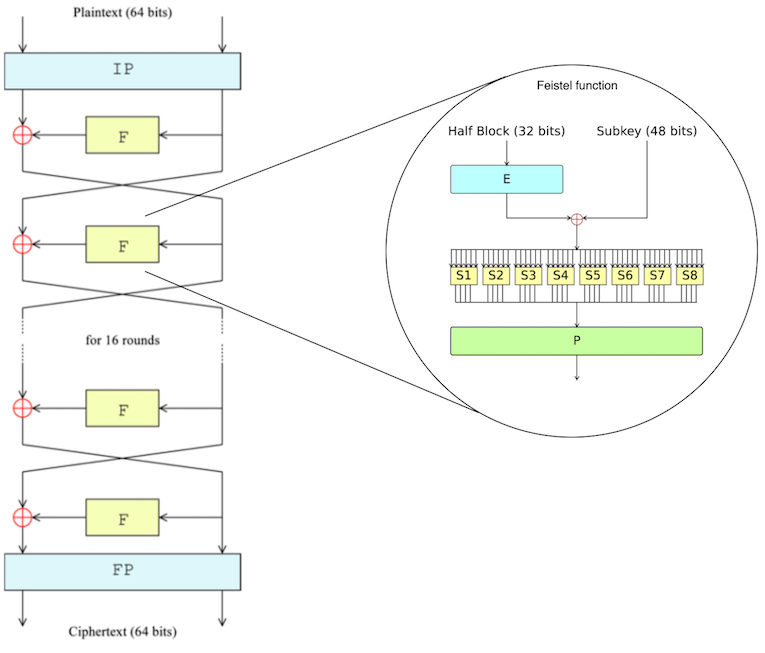
Inspecting the flow of the DES algorithm, it can be seen that the 64-bits plaintext input is split into two parts of 32-bits each. At the beginning of the algorithm, an initial permutation of both parts is performed, and then the 32-bits block that is in the right side in that round enters the Feistel function. Finally, the output of the Feistel function is XORed with the left side and a new round starts switching sides. After the sixteenth round, the output is subjected to a final permutation to obtain the final 64-bits ciphertext.

Taking a look inside the Feistel function, the following steps can be seen:

1. Expansion: the 32-bit half-block is expanded to 48 bits using the expansion permutation, denoted E in the diagram, by duplicating half of the bits.
2. Key mixing: the result is combined with a subkey using an XOR operation.
3. Substitution: after mixing in the subkey, the block is divided into eight 6-bit pieces before processing by the substitution boxes (S-boxes). Each of the eight S-boxes replaces its six input bits with four output bits according to a non-linear transformation, provided in the form of a lookup table.
4. Permutation: The 32-bit output from the S-boxes are rearranged according to a fixed permutation, the P-box. This is designed so that, after permutation, the bits from the output of each S-box in this round are spread across four different S-boxes in the next round.

Differential Fault Analysis

This attack is based on the statistical analysis of an original trace (execution trace of a successful encryption of a given input) together with traces obtained using the same input and injecting faults during its execution. In the hardware version of this attack the faults can be injected through different techniques such as power glitches or light pulses from a laser. In the software version the faults are injected using dynamic binary instrumentation, which requires control over the execution environment. For this type of attack, it is required to execute the cryptographic algorithm several times with the same input in order to obtain information leakages when faults at different points of the execution are injected.

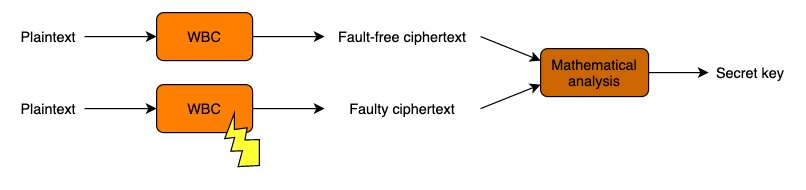
With the knowledge about the algorithm explained above, we can explore how this attack is applied for the DES algorithm. The equation that illustrates each round of the algorithm is as follows:

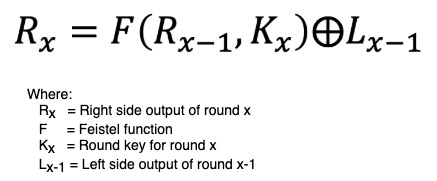
For an intermediate round the value of each one of the variables in the formula is unknown. However, when it comes to the last round the values of R16 and R16-1 will be known because they will be part of the final output of the algorithm if the final permutation, which is known, is reversed. Therefore, the equation will only have two unknown values for the attacker (K16 and L15). By performing again the same encryption process with the same input, but injecting a fault to alter 1-bit while the Feistel function of the last round is computed we can remove the L15 value applying the following formula:

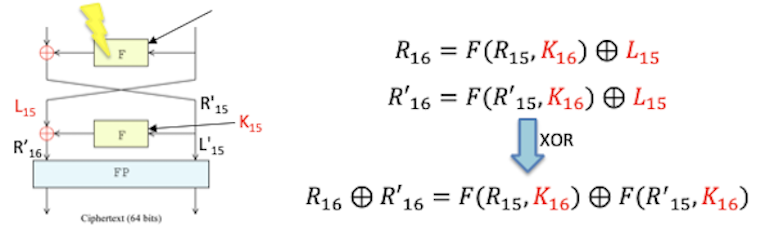
Now that the only unknown variable in the formula is the round key for the sixteenth round, it is still necessary to resolve the equation to obtain the value for K16. It is possible to do this by abusing of the S-boxes in the Feistel function. Since the structure of the S-boxes is known, the input can be brute-forced until the same output is obtained. An additional advantage of this approach is that the S-boxes take only 6 bits as input, so they can be brute-forced separately applying a “divide and conquer” approach.

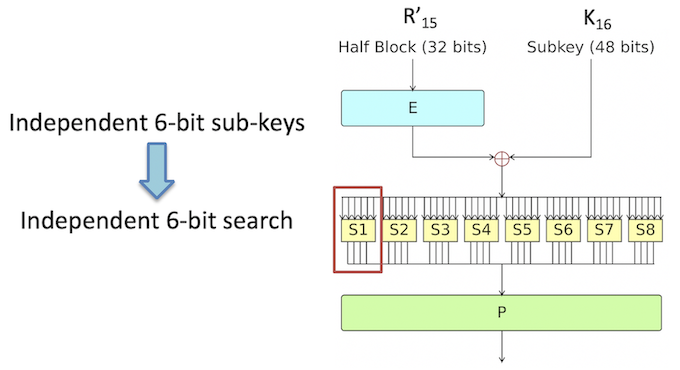
Because of the information loss in the S-boxes, it is necessary to perform this process several times with different faulty outputs to find the solution to this equation that is repeated the highest number of times, giving the correct candidate solution for each S-box. As result of all these steps, the sixteenth round key will be revealed.

To reverse DES’ key scheduling process it is necessary to have two round keys at least. By applying the formula seen before to the fifteenth round and substituting the results obtained from the previous step, the equation is now solvable, allowing to perform the same process again to retrieve this round key.

With the last two round keys retrieved, it is possible to apply the reverse key scheduling process to retrieve the original DES encryption key that was embedded in the White-Box Cryptography implementation.

Differential Computational Analysis

This attack is based on the statistical analysis of several execution traces of the same White-Box Cryptography implementation with different given inputs and a collection of educated guesses to find correlation between the intermediate values generated by the original traces and the "synthetically" generated values. In the hardware version of this attack, the power consumption of the CPU is traced to determine which types of mathematical operations (addition, multiplication, etc.) were performed to determine the intermediate values that were generated by the algorithm. Fortunately, in the case of software this conversion is not needed since the values handled by the CPU and memory can be directly inspected.

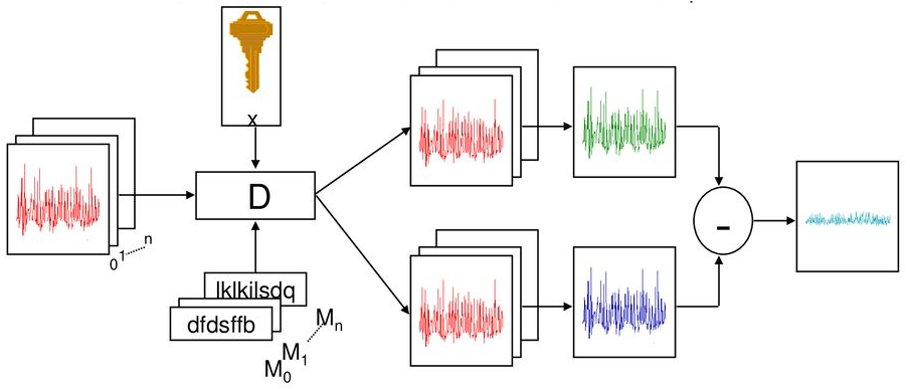
Taking the DES algorithm and the S-boxes already explained previously, this attack is focused on the first round of the algorithm, more specifically in the intermediate results generated after the first Feistel function. Because the input is controlled and the operations performed inside of the Feistel function are publicly known, it is possible to emulate this behavior for every possible first round key. However, 2^48 permutations are too many to be brute-forced.

The result of each S-box has a direct impact in the final result of the round output. By taking again the “Divide and conquer” approach, if each S-box can be brute-forced until a correct value for the hypothetical round key matches the measurements obtained from the execution traces.

Like the previous attack, the loss of information at the S-boxes that this process is executed several times, while checking with execution traces of different inputs to discard wrong guessed round keys.

Once the first-round key is extracted, the process to retrieve the second one is again the same, using the correct value for the first round key to generate correct intermediate values to feed the input of the second round, generating new guesses and performing the analysis again.

Does it mean that White-Box Cryptography is weak?

The attacks explained above are quite powerful, and have the advantage that, compared with their hardware analogs, with DCA and DFA it is possible to retrieve the encryption key with a few execution traces. Since these attacks were discovered, the idea of White-Box Cryptography became not enough to defend software against privileged attackers, making necessary to add defensive countermeasures to its structure to make it resistant to attacks.

A clear example of the actual power of these attacks can be seen in the biggest White-Box Cryptography contest run at CHES conference, where developers and attackers fight for creating the strongest implementation and breaking them. Most of the implementations created in the last contest were cracked, and some of them in less than one week.

However, it would not be fair to base the judgment about the security of this technology only on these results, where the White-Box Cryptography implementations are already isolated and designed to be easily traced and attack. The truth is that in real-world scenarios White-Box Cryptography is extremely secure. When an attacker faces a real-world app that is making use of White-Box Cryptography, it is unknown the encryption algorithm that it is implementing where it is located inside the binary, and furthermore, it is usually protected by many other countermeasures.

White-Box Cryptography protection

A wide range of security countermeasures can be applied to harden a White-Box Cryptography implementation.

Specific countermeasures that can be applied on the White-Box Cryptography implementation are:

• Device binding: When the White-Box Cryptography instance is initialized when the application is launched the first time, it is possible to substitute part of the random data that will be inserted into the lookup tables with specific data from the device where it was installed (e.g. IMEI number of the mobile device). Later on, the White-Box Cryptography instance will verify that the device where it is running has the same unique identifier, making harder to extract it to be run isolated in an emulator to extract execution traces.
• Encoding: As explained before, the DCA and DFA attacks are based in the collection and mathematical analysis of the differences between the input/output and the intermediate states of data while it is being processed by the White-Box Cryptography. If this data is encoded, these values will not be valid for its analysis. Two types of encoded can be implemented:
  • External: It is based on the encoding of the input and output of the White-Box Cryptography implementation. The input has to be supplied with the proper encoding that is embedded inside the White-Box Cryptography instance, and the output returned is also encoded.
  • Internal: It is based in the encoding of the intermediate states of the algorithm. In each lookup table, the data is first decoded, processed and then encoded again before being sent to the next one.

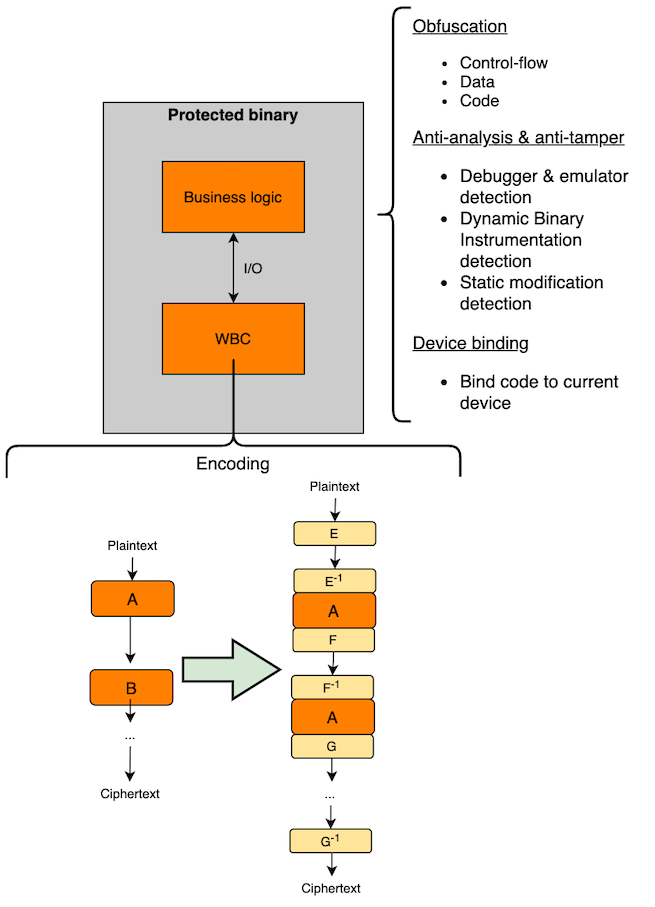
• Periodical updates: Periodical renewal of the embedded encryption keys makes useless the entire effort of attackers to find, isolate and analyze the White-Box Cryptography implementation. In case these updates do not stop an attacker to retrieve the encryption key, it will minimize the impact of the security breach.

In addition to these White-Box Cryptography countermeasures, it is important to remember that at the end of the day it is software like any other component in an application, and therefore the same security measures can be applied to add a second layer of protection and make harder the work of finding and isolating the White-Box Cryptography instance. Some of these techniques are:

• Data obfuscation
• Code Obfuscation
• Control-flow obfuscation
• Anti-tampering
• Detection of debuggers and emulators
• Detection of dynamic binary instrumentation attacks

Conclusion

White-Box Cryptography is a great security mechanism to protect the cryptography executed on open devices that do not have secure cryptographic hardware support and are handled by potential attackers.

As any other security measure, it is susceptible to attacks. However, White-Box Cryptography has proven its resistance against attacks in real-world scenarios where it is integrated with many other countermeasures.

For these reasons, at Securify we strongly believe that the usage of this type of cryptographic techniques will be eventually implemented in every mobile app handling cryptography, and we are already working on it to bring the best approach for efficient and quality testing of White-Box Cryptography.

Thanks for reading.